Ein Formalismus zur Beschreibung von Token-Systemen

Das Web3 hat vielen Begriffen der Finanzwirtschaft eine erweiterte Bedeutung gegeben, die zu Missverständnissen führen kann. Dem begegnend wird in vorliegendem Artikel eine präzise Formalisierung anhand der fundamentalen Funktionen von Blockchains und Token auf Basis des ERC20 ausgearbeitet. Dieser Standard beschreibt die am weitesten verbreiteten Funktionalitäten von Blockchains für fungible Tokens:

• ERC20.symbol() gibt das Symbol des Tokens aus.
• ERC20.balanceOf(address) gibt den Kontostand der Adresse an.
• ERC20.transfer(receiver, amount) transferiert die gegebene Menge Token von der nicht angeführten Adresse des Funktionsaufrufers zur angegeben Empfängeradresse.
• ERC20.totalSupply() gibt die Gesamtmenge der verfügbaren Token an.

Notationskonventionen

Die hier eingeführte Notation basiert auf 4 Indizes, die an verschiedenen Positionen platziert sein können. Es werden sowohl linke, als auch rechte obere und untere Indizes verwendet. Das resultierende Objekt besteht damit aus 5 Bestandteile, $\;_\square^\square\Box_\square^\square$ und ist insgesamt als Platzhalter für eine einzelne Zahl zu verstehen.

Token, Benutzer und Adressen

Als synonym betrachten wir:

• Token-Symbol und Token-Adresse, z.B. DAI und 0x6b175474e89094c44da98b954eedeac495271d0f . Diese werden als rechte untere oder oberen Indizes mit lateinischen Kleinbuchstaben ("$i$") angegeben.
• Benutzer, ihnen zugeordnete Adressen und Adressen von nicht Token-Erzeugenden Smart Contracts (z.B. "Pools"). Diese werden als linke untere oder obere Indizes mit griechischen Kleinbuchstaben ("$\alpha$") angegeben.

Kontostände

Kontostände beziehen sich immer auf einen Token $i$, einen Benutzer $\alpha$, sowie die Blockzeit $t$ und werden angeschrieben als:

$\;^\alpha A_i[t]$

Dies bezeichnet den Kontostand an Token $i$ des Benutzers $\alpha$ zur Zeit $t$, entspricht also einem Aufruf der Funktion ERC20(i).balanceOf(alpha), wobei alpha gleich $\alpha$ ist. Der Großbuchstabe "A" steht für arbiträre Asset- oder Variabel-Typen. Wenn eine explizite Angabe des Types erforderlich ist, kann er ersetzt werden durch:

• "N" für natürliche Zahlen (ganze Zahlen).
• "R" für reele Zahlen (dezimale Zahlen).
• "B" für boolsche Größen (True/False).

Wenn bereits aus dem Kontext ersichtlich, können Blockzeit und Indizes weggelassen oder ein expliziter Token oder Benutzer ausgeschrieben werden: Betrachten wir einen Uniswap Pool mit ganzzahligen Kontoständen für MATIC und DAI, so schreiben wir die zwei relevanten Kontostände des Pools als $\;^\text{Uni} N_\text{DAI}$ und $\;^\text{Uni} N_\text{MATIC}$ an.

Transfers, Zustandsänderungen

Transfers, Erzeugung und Vernichtung von Token bedingen Zustandsänderungen, die wir als Abfolge zeitabhängiger Kontostände auffassen:

$\;^\alpha A_i[0] \rightarrow \;^\alpha A_i[1] \rightarrow ... \;^\alpha A_i[t] \rightarrow \;^\alpha A_i[t+1] $

Die einzelne Zustandsänderung kann verkürzt angeschrieben werden, indem die Zeit-variabel $t$ weggelassen und stattdessen der neue Zustand mit einem Strich markiert wird:

$\;^\alpha A_i \rightarrow \;^\alpha A_i' $

Für einen Token-Transfer müssen zwei Kontostände geändert werden: Der Kontostand des Senders $\alpha$ wird um die zu transferierende Menge $M$ reduziert und der Kontostand des Empfängers $\beta$ um die gleiche Menge erhöht:

$\;^\alpha A_i' = \;^\alpha A_i - M $

$\;^\beta A_i' = \;^\beta A_i + M$

Um eindeutig und unverwechselbar anzuschreiben, welcher Zustand sich wie ändert, führen wir ein $\Delta$ ein, dass dem sich ändernden Zustand vorangestellt wird. Für die zuvor angeschriebenen Zustandsänderungen gilt daher:

$ \Delta \;^\alpha A_i' = - M $

$ \Delta \;^\beta A_i' = M$

Unter Annahme der Erhaltung der Gesamtmenge eines betrachteten Tokens muss jeder bei einer Adresse verschwindende Token bei einer anderen auftauchen, also immer Sender und Empfänger definiert sein. Um dies explizit anzuschreiben, fügen wir den Empfänger explizit als unteren Index hinzu hinzu $\Delta\;^\alpha_\beta A_i$. Es gilt:

$\Delta\;^\alpha_\beta A_i = -\Delta\;^\beta_\alpha A_i = -M$

Damit sind die beiden Kontostandsänderungen eines Transfers zusammengefasst und wir sprechen von einem Fluss des Tokens $i$ von $\alpha$ zu $\beta$. Als Eselsbrücke kann man sich einen rechten Winkel vorstellen, der beim Index des transferierten Tokens beginnt, nach links zur Senderadresse läuft und dann nach oben zur Empfängeradresse zeigt: $\uparrow\underleftarrow{\Delta\;^\alpha_\beta A_i}$

Token-Flüsse und auch allgemeinere Zustandsänderungen sind auf Etthereum-artigen Blockchains als Funktionen eines Smart Contractes implementiert und damit meist einem Token zugeordnet. Unsere Notation sei am Beispiels der Transfer-Funktion des DAI veranschaulicht, die die Token-Menge $M$ von $\alpha$ zu $\beta$ tranferiert, wobei auch der Sender explizit angeführt ist:

$\text{DAI.transfer}(\alpha, \beta, M)\{$

$\;^\alpha A_\text{DAI}' = \;^\alpha A_\text{DAI} - M;$

$\;^\beta A_\text{DAI}' = \;^\beta A_\text{DAI} + M;$

$\} $

Oder in kompakterer Form:

$\text{DAI.transfer}(\alpha, \beta, M)\{$

$\Delta^\alpha_\beta A_\text{DAI} = -M;$

$\} $

Wir führen zuerst den Relevanten Token an, dem die Funktion zugeordnet ist, dann nach einem Punkt die Funktion, in runden Klammern die Parameter und in geschwungenen Klammern die Zustandsänderung: Adresse.Funktion(Parameter){Zustandsänderungen} Dabei sind die Zustandsänderungen über Auflistungen der Form "A' = f(A, ...)" oder die Deltas anführbar. Die Funktion "f(A,...)" wird als Übergangsfunktion bezeichnet: Sie übernimmt die "alten" Variablen und errechnet daraus jeweils eine "neue" Variable. Alternativ kann auch die sogenannte, später erörterte Invarianz angegeben werden.

Erzeugung/Vernichtung und Gesamtmenge

Erzeugung (Minting) und Vernichtung (Burning) von Token kann als Transfer von und zu einer Nulladresse aufgefasst werden: Erzeugung von Token an der Adresse $\alpha$ entspricht einem positiven $\Delta\;^\alpha_0 A_i$ und Vernichtung einem positivem $\Delta\;^0_\alpha A_i$. Die Gesamtmenge eines gegebenen Token $i$ schreiben wir an als "$-\;^{0} A_i$", was ERC20(i).totalSupply() entspricht. Wir nehmen also an, dass die Nulladresse einen negativen Kontostand hat, der der Summe aller anderen Kontostände entspricht. Es gilt also:

$\underbrace{\sum_{\alpha \neq 0} \; \;^\alpha A_i}_{\begin{array}{l}\text{Summe aller Kontostände}\\\text{exklusive Nulladresse}\end{array}} + \overbrace{\;^{0} A_i}^\text{Kontostand der Nulladresse} = \underbrace{\sum_{\alpha} \; \;^\alpha A_i}_{\begin{array}{l}\text{Summe aller Kontostände}\\\text{inklusive Nulladresse}\end{array}} = 0$

Dabei werden in der ersten Summe alle Kontostände exklusive jenes der Nulladresse summiert, die separat aufaddiert wird. Die Summe auf der rechten Seite umfasst alle Kontostände inklusive jenes der Nulladresse. Vorausgreifend kann angemerkt werden, das oben angeführter Zusammenhang, also $\sum_{\alpha} \; \;^\alpha A_i = 0$, die Invarianz von Minting und Burning Ereignissen sowie Transfers darstellt.

Das Preisfunktional

Preise und Tokenbewegungen sind korreliert. Der Fluss von Token von einer Adresse zu einer von dieser unabhängigen Adresse, wird im Allgemeinen durch einen entgegengerichteten Token-Fluss oder Ressourcenfluss kompensiert: Werden Token $i$ von $\alpha$ zu $\beta$ transferiert, kann angenommen, dass eine dazu wertgleiche Menge anderer Token $k$ als Ausgleich von $\beta$ zu $\alpha$ transferiert wird. Entsprechend gibt es zu $\Delta\;^\alpha_\beta A_i$ einen Token $k$ mit nicht verschwindendem $\Delta\;^\beta_\alpha A_k$ und die beiden Token-Flüsse sind proportional zueinander. Als Proportionalitätsfaktor führen wir das Preisfunktional $ \;_\beta^\alpha p_k^i\;$ ein. Es gibt an, wieviele Token $k$ in einem Handel zwischen Benutzer $\alpha$ und Benutzer $\beta$ wievielen Token $i$ entsprechen, wenn die Token $i$ von $\alpha$ zu $\beta$ fließen und die Token $k$ von $\beta$ zu $\alpha$: Die Richtung des Handels ist also von Relevanz und die zwei gekoppelten Flüsse können ergeben sich über folgende Eselsbrücke:

$\underbrace{\uparrow\underleftarrow{\;_\beta^\alpha p_k^i\;}}_{\text{k von }\beta\text{ zu }\alpha}\quad\text{ und }\quad\overbrace{\downarrow\overleftarrow{\;_\beta^\alpha p_k^i\;}}^{\text{i von }\alpha\text{ zu }\beta}$

Damit entspricht das Preisfunktional einer Kopplung zweier, sich hinsichtlich Wert kompensierender, entgegengesetzter Token-Flüsse und wir schreiben:

$\Delta\;^\alpha_\beta A_k = \;_\beta^\alpha p_k^i\; \Delta\;^\beta_\alpha A_i $

Es bezeichnet $ \;_\beta^\alpha p_k^i\;$ den Wert der Token $i$ auf Adresse $\alpha$ aus Sicht der Adresse $\beta$ nominiert in Token $k$ - pointierter formuliert: wieviel mir ("$\beta$ ") das Auto ("$i$") meines Nachbarn ("$\alpha$") bemessen in Birnen ("$k$") wert ist. Da die gleichen Flüsse auch durch $-\Delta\;^\beta_\alpha A_i = -\;_\alpha^\beta p_i^k\; \Delta\;^\alpha_\beta A_i $ beschreibbar sind, entspricht das Austauschen oberer und unterer Indizes des Preisfunktionals einer Inversion:

$ \;_\beta^\alpha p_k^i = \frac{1}{\;_\alpha^\beta p_i^k} $

Man beachte, wie obere und untere Indizes zueinander finden und das Preisfunktional einen Indexwechsel in den Flüssen bedingt: Ein oberer Index des Preisfunktionals, der auf einen gleichen unteren Index im Fluss trifft, ersetzt diesen durch den entsprechenden unteren Index des Preisfunktionals. Ebenso ersetzt ein unterer Index des Preisfunktionals, der auf einen gleichen oberen Index im Fluss trifft, diesen durch den entsprechenden oberen Index des Preisfunktionals. Dies ist insofern relevant, als nur Kontostände gleichen Tokens miteinander verglichen werden können, die Multiplikation mit dem Preisfunktional aber eine Umrechnung ermöglicht. Angenommen wir wollen den Wert eins Portfolios, umfassend $A_\text{UNI}$ UNI und $A_\text{MATIC}$ MATIC in DAI (also $) angeben, wobei wir die Preise von einem dezentralen Marktplatz (DEX) wie z.B. BAL (Balancer) beziehen, dann ergibt sich der Wert zu:

$\text{Portfoliowert =}\; \;_\text{BAL} p_\text{DAI}^\text{UNI} * A_\text{UNI} + \;_\text{BAL} p_\text{DAI}^\text{MATIC} * A_\text{MATIC} $

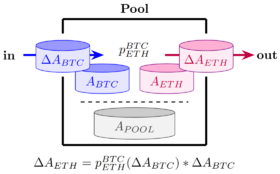
Hierbei haben wir den oberen linken Index weggelassen, da ein Marktpreis unabhängig davon ist, auf welcher Adresse das betrachtete Asset liegt: Bei einem Pool $\alpha$ ist der Preis im Normalfall unabhängig vom jeweiligen Benutzer, es gilt also für alle $\gamma$ und $\beta$ dass $\;_\alpha^\beta p_k^i\; = \;_\alpha^\gamma p_k^i\;$. In solchem Fall kann der obere linke Index weggelassen werden und wir schreiben $\;_\alpha p_k^i\;$ für den Wert des Token $i$ nominiert in Token $k$ anhand der Preise des Pools mit Adresse $\alpha$. Dies gibt an, wieviel von Token $k$ man für einen Token $i$ vom Pool $\alpha$ bekommt:

In der Grafik bezeichnet $A_\text{POOL}$ den Liquidity-Token des Pools, dessen Wert durch die im Pool befindlichen $A_\text{BTC}$ und $A_\text{ETH}$ gedeckt ist.

Das Preisfunktional ist derart allgemein formuliert, dass es sämtliche verbreitete Preisdefinitionen umfasst, jedoch deutlich über diese hinausgehen kann und muss: Es ist nötig, auch subjektive Werteinschätzungen abzubilden. Dazu ziehen wir den Wert bemessen in beliebigem Asset $i$ heran, das ein Benutzer $\alpha$ bereit ist, zu vernichten, um ein anderes Asset $k$ zu erzeugen und schreiben dies wie folgt an:

$ \;_0^\alpha p_k^i$

Wir führen die subjektive Werteinschätzung also auf den Preis einer Token-Prägung (minting) zurück: diese gibt an, wieviel jemand zu geben bereit ist, um ein bestimmtes Gut zu erhalten. Demgegenüber gibt $ \;_\beta^0 p_k^i$ an, welchen Ausgleich bemessen in $k$ eine Person $\alpha$ fordert, um sich von einem Asset $i$ zu trennen. Wenn zwei subjektive Werteinschätzungen kompatibel zueinander sind, kann ein Tausch zu Stande kommen, es gilt dann: $ \;_0^\alpha p_i^k  \;_\beta^0 p_i^k =  \;_\beta^\alpha p_i^k$

Das Preisfunktional ist im Allgemeinen keine Konstante, sondern kann, unter Anderem, von $\Delta\;^\alpha_\beta A_i$ abhängen: $\;_\alpha^\beta p_k^i(\Delta\;^\alpha_\beta A_i)$. Diese Abhängigkeit des Preises von der Tradesize bedingt, dass man mit wachsender Tradesize meist einen schlechteren Preis bekommt. Dies wird hier als Slippage (Preisrutsch) bezeichnet und später detaillierter behandelt.

Liquiditäts-Token

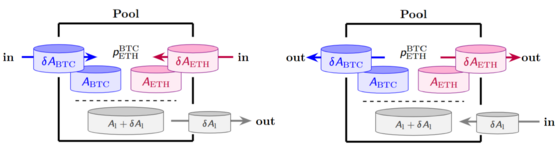
Der Liquiditäts-Token wurde in den vorherigen Bildern bereits als $A_\text{Pool}$, bzw. $A_\text{Pool1}$ und $A_\text{Pool1}$ dargestellt und entspricht dem vom Pool herausgegeben Token, also einer Beteiligung am jeweiligen Pool. Wir schreiben zur Abkürzung den Liquiditätstoken des Pools nun als $A_l$ an. Der Anteil einer Adresse $\alpha$ am Pool $\gamma$ ist gegeben durch den Kontostand $\;^\alpha A_l$ von $\alpha$ geteilt durch die Gesamtmenge $-\;^{0} A_l$, also:

$\text{Anteil von }\alpha \quad = \quad -\frac{\;^\alpha A_l}{\;^{0} A_l}$

Liquiditäts-Token kann man in Austausch einer oder mehrerer der im Pool enthaltene Token erhalten (siehe linke Seite nachfolgender Abbildung). Bei ihrer Rückgabe erhält man die im Pool enthaltenen Token in Menge des Anteils, dem die zugeführten Liquiditäts-Token entsprechen (siehe rechte Seite der Abbildung).

Bei den bisher betrachteten Transaktionen waren nur zwei verschiedene Token beteiligt. Dies wird bei Liquiditäts-Transaktionen verallgemeinert: eine beliebige Anzahl verschiedener Token kann dabei bewegt werden. Das hat zur Folge, dass kein eindeutiger Preis definierbar und daher eine Verallgemeinerung des Preisfunktionals nötig ist, die jedoch den Rahmen vorliegenden Artikels sprengen würde.

Der Preis des Liquiditätstokens ist in der Regel nach unten durch den Wert des Pools besichert, wobei folgend der Einfachheit halber Dollar-Preise herangezogen werden:

$p^\text{l}_\text{\$} \geq \; -\frac{p^\text{BTC}_\text{\$} * \;^\text{Pool} A_\text{BTC} +  p^\text{ETH}_\text{\$} * \;^\text{Pool} A_\text{ETH}}{\;^{0} A_l} $

Das negative Vorzeichen resultiert aus dem Vorzeichen der Gesamtmenge $-\;^{0} A_l$. Diese untere Grenze des Preises eines Liquiditätstoken ist anfällig für Impermanent Loss, worauf später näher eingegangen wird.

Wichtige Zusammenhänge

Die zuvor beschriebene Notation erlaubt, Token-Systeme "statisch" zu beschreiben. Die "Statik" eines Token-Systems lässt sich in einer einzigen Größe darstellen: Der Invarianz des Systems.

Invarianzen

Invarianzen eines Systems erlauben, alle möglichen Zustände des Systems auf einmal zu analysieren, was jedoch ein hohes, mathematisches Verständnis erfordert. In vorliegender Notation werden Invarianzen mit einem große, kalligraphischen $\mathcal{I}_\text{Zustandsänderung}$ angeschrieben, wobei die jeweils zugeordente Zustandsänderung als rechter, unterer Index angeführt wird. Es handelt sich bei Invarianzen um Größen, die bei Zustandsänderungen unverändert bleiben, aber dezidiert aus den sich Ändernden Zuständen gebildet sind. Eine Invarianz beschreibt die Zustandsänderung genauso umfassend, wie es die Übergangsfunktionen tun, die sich direkt aus der Invarianz bestimmen lassen. Beispielsweise ist die Invarianz eines Token-Transfers, also eines Flusses $\Delta\;^\beta_\alpha A_i=M$ gegeben durch $\mathcal{I}_\text{Transfer}=\;^\alpha A_i+\;^\beta A_i$, also der Summe der Kontostände von Absender- und Empfängeradresse. Es gilt dann:

$\mathcal{I}_\text{Transfer}=\;^\alpha A_i+\;^\beta A_i = (\underbrace{\;^\alpha A_i+M}_{\;^\alpha A_i'})+(\underbrace{\;^\beta A_i-M}_{\;^\beta A_i'})=\mathcal{I}'_\text{Transfer}$

Die Menge der Token ist vor dem Transfer gleich der Menge nach dem Transfer. Im ausgearbeiteten Formalismus lässt sich diese Invarianz leicht auf Minting- und Burning-Events ausweite:

$\mathcal{I}_\text{MintBurnTransfer} = \sum_\alpha \;^\alpha A_i = 0$

Invarianz, Übergangsfunktion und Preisfunktional stehen miteinander in engem Zusammenhang, wie folgend am Beispiel von UniSwap ausgeführt wird:

$\underbrace{\mathcal{I}_\text{Uni}= A_i * A_k}_\text{Invarianz} \;\Leftrightarrow\; \underbrace{\Delta A_i = -A_i \frac{\Delta A_k}{A_k+\Delta A_k}}_\text{Übergangsfunktion} \;\Leftrightarrow\; \underbrace{\;^\text{Uni} p_i^k(\Delta A_k) = \frac{ A_i}{A_k+\Delta A_k}}_\text{Preisfunktional}$

Die Übergangsfunktion ergibt sich aus folgender Überlegung: Man ändert eine Variabel $A_k \rightarrow A_k' = A_k+\Delta A_k$, um die daraus resultierende Änderung der Invarianz durch Änderung einer anderen Variablen $A_i \rightarrow A_i' = A_i+\Delta A_i$ wieder auszugleichen. Dadurch wird eine Variabeländerung $\Delta A_k$ mit einer anderen $\Delta A_i$ verknüpft, was direkt der Übergangsfunktion entspricht. Das Preisfunktional ist aus dem negativen Verhältnis der Änderungen, $-\frac{\Delta A_i}{\Delta A_k}$, bestimmbar. Im Grenzübergang verschwindender Variabeländerungen wird daraus eine Ableitung, die über eine implizite Ableitung mit der Invarianz ausgedrückt werden kann:

$ p_i^k = - \frac{\partial A_i}{\partial A_k} = \frac{\frac{\partial \mathcal{I}}{\partial A_k }}{\frac{\partial \mathcal{I}}{\partial A_i}} $

Folgend betrachten wir die Dynamik des Systems, also die Interaktionen von Preisen und Token-Flüssen und welche Gesetzmäßigkeiten diesen zu Grunde liegen

Markttreibende Kräfte

Die Natur, bzw. Physik strebt stets eine Minimierung der Energie an. Durch Minimierung eines Energiefunktionals lässts ich eine Vielzahl an Naturphänomenen erklären und vorhersagen. Wir suchen nun hierzu vergleichbare Größen, deren Minimierung ein Token-System anstrebt und sprechen von Markttreibenden Kräften. Bei Minimierung der gesuchten Größen bedingen Preisdifferenzen und Token-Flüsse einander, wobei die Invarianzen erhalten bleiben. Der einfachste Fall liegt vor, wenn zwei Personen $\alpha$ und $\beta$ sich auf einen Handel einigen, bei dem die Personen ein Asset $i$ gegen ein Asset $k$ tauschen. Folgend werden die treibenden Kräfte derartigen Tausches formalisiert:

$\overbrace{\;_\alpha^0 p_k^i > 1}^{\alpha \text{ möchte } k \text{ und gibt } i} \text{ und } \underbrace{\;_\beta^0 p_i^k > 1}_{\beta \text{ möchte } i \text{ und gibt } k} \Rightarrow\quad \Delta\;^\alpha_\beta A_i > 0 \text{ und } \Delta\;^\beta_\alpha A_k>0$

Ein Handel kommt zu Stande, wenn sich beide auf einen Preis einigen, also jeder an die Stelle des "0" beim jeweils anderen treten kann. Es gelten dann folgende Identitäten:

$\;_\alpha^0 p_k^i = \frac{1}{\;_\beta^0 p_i^k} = \;_0^\beta p_k^i=\;_\alpha^\beta p_k^i = \frac{ \Delta\;^\beta_\alpha A_k}{ \Delta\;^\alpha_\beta A_i}$

Dabei werden die Flüsse $\Delta\;^\beta_\alpha A_k$ und $\Delta\;^\alpha_\beta A_i$, bzw. der Preis $\;_\alpha^\beta p_k^i$ realisiert. Diese resultieren daher, dass die beiden Personen den Assets einen verschiedenen Wert beimessen und beide am Tausch eine subjektive Wertsteigerung erfahren. Die Maximale Wertsteigerung ist erreicht, wenn $\;_\alpha^0 p_k^i=1$, wenn also alle Güter derart verteilt sind, sodass die subjektiven Werteinschätzungen minimalen Abstand zur 1 haben, also: $\text{Min}(|\;_\alpha^0 p_k^i-1|)$. Die subjektiven Bewertungen können durch Stakeholderanalysen, bzw. Projektumfeldanalysen zumindest statistisch für systemrelevante Interessengruppen erfasst werden.

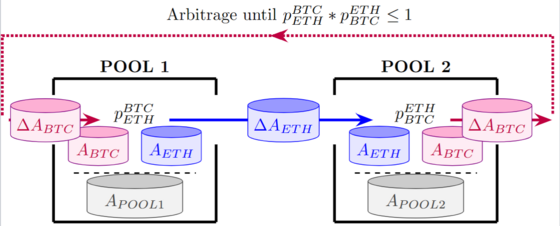
Besser erfassbar ist der Zusammenhang von Preisunterschieden und Token-Flüssen. Treten bei verschiedenen Pools zu gleichem Asset abweichende Preise auf, so sind dadurch Token-Flüsse verursacht bis es zu einem Preisangleich kommt. Dies bezeichnen wir als Arbitrage: Dabei betrachtet ein Arbitrageur $\gamma$ den Preis zwischen zwei Assets $i$ und $k$ an zwei verschiedenen Pools $\alpha$ und $\beta$, um aus Preisunterschieden Profit schlagen zu können: billig kaufen, um direkt darauf teuer zu verkaufen. Eine derartige Arbitrage-Möglichkeit verrät sich durch folgenden Zusammenhang:

$\;_\gamma^\alpha p_k^i\; * \;_\gamma^\beta p_i^k\; > 1 $

Dieser ist folgend am Beispiel von BTC und ETH veranschaulicht: Arbitrage Möglichkeiten erlauben, Profit zu erhandeln.

Wird eine derartige Profit-Möglichkeit von einem Arbitrageur $\gamma$ wahrgenommen, sind die folgenden Token Flüsse zu bemerken: Der Arbitrageur transferiert Token $k$ zu einem Pool $\beta$, also $\Delta\;^\beta_\gamma A_k > 0$. Der Arbitrageur empfängt dafür eine entsprechende Menge an Token $i$ vom Pool, also, $\Delta\;^\gamma_\beta A_i > 0$. Darauf hin Swapt er in umgekehrte Richtung an einem anderen Pool $\alpha$, entsprechend zu $\Delta\;^\alpha_\gamma A_i > 0$ und $\Delta\;^\gamma_\alpha A_k > 0$. Da derartige Arbitrage-Möglichkeiten mit längerer Zeit ihres Bestehens zusehends wahrscheinlicher genutzt werden, tendieren Token-Systeme dazu, Folgende Größe zu Minimieren:

$\text{Min}(|\;_\gamma^\alpha p_k^i\; * \;_\gamma^\beta p_i^k\;-1|)$

Alle $\;_\gamma^\alpha p_k^i\; * \;_\gamma^\beta p_i^k$ tendieren also zur 1.

Arbitrage zwischen zwei Pools bedingt in der Regel eine meist nach unten gerichtete Preis-Schwankung der Liquiditäts-Token beider Pools. Der damit einhergehende Wertverlust wird als Impermanent Loss bezeichnet und kann mit der Slippage und Liquidität beider Pools in Zusammenhang gebracht werden.

Im Allgemeinen ist es nicht oder nur mit größtem Aufwand möglich, die optimale Tradesize zu finden, um maximalen Profit und ein direktes Schließen von Preislücken (also $\;_\gamma^\alpha p_k^i\; * \;_\gamma^\beta p_i^k$=1 ) mit einem einzigen Arbitrage-Trade zu erreichen. Eine zu niedrige Tradesize führt dazu, dass die Preisdifferenz nicht vollständig abgebaut wird und damit weiterhin einer Arbitrage-Möglichkeit bestehen bleibt. Mit zu hoher Tradesize überschießt man die Preislücke und öffnet eine Arbitrage-Möglichkeit in die andere Richtung. Da eine Vielzahl an Arbitrageuren darum konkurrieren, die Arbitrage-Möglichkeiten zu nutzen und sie sich dabei "in die Quere kommen", sind zufällige Preisbewegungen zu erwarten. Bei extern bedingten Preisänderungen ist daher beim Preisangleich ein Überschwingungen zu erwarten.

Die genannten markttreibenden Kräfte zwingen das System dazu, sich nach und nach den genannten Minima unter Erhaltung der Invarianzen anzunähern. Bei der Entwicklung von Token-Systemen ist darauf zu achten, dass sie weder am Weg zu diesen Minima noch an den Minima selbst unerwünschtes Verhalten aufweisen. Unerwünschtes Verhalten kann beispielsweise in zu hoher Slippage oder zu hohem Impermanent Loss bestehen. Die Minimierung der beiden stellt in der Regel einen Zielkonflikt dar.

Slippage (Preisrutsch)

Slippage ist der Unterschied zwischen angegebenem ("spot-price") und realisiertem Preis und hat zwei Ursachen:

• Hohe Volatilität, bei der der Preis zu einem "bewegten Ziel" wird und sich während des Trades ändert. Hierbei wird der Preis nicht aufgrund des Trades sondern unabhängig von diesem und in der Regel zufällig verändert.
• Geringe Liquidität, wodurch sich der Preis mit wachsender Tradesize aufgrund des Trades verändert. Hierbei ist der Trade die direkte Ursache der Preisänderung und der realisierte Preis verschlechtert sich mit größer werdender Tradesize.

Slippage bringt Token-Flüsse mit Preisänderungen in Zusammenhang und stellt damit auch ein Maß für die Fragilität des Token-Systems dar: Bei hoher Slippage reagiert das System mit starken Preisänderungen auf Token-Flüsse, aber mit schwachen Token-Flüssen auf Preisänderungen. Bei niedriger Slippage ist es umgekehrt. Damit hängt auch von der Slippage ab, wie das Token-System auf Volatilität reagiert.

Mit wachsender Tradesize $\Delta A_k$ tritt in der Regel bei Liquiditäts-Pools eine Verschlechterung des Preise von $p_i^k(0)$ auf ein $p_i^k(\Delta A_k) \; < \; p_i^k(0)$ ein, die Preisänderung beträgt also $p_i^k(\Delta A_k)-p_i^k(0)$. Die Slippage $s_i^k$ beschreibt, wie stark diese Verschlechterung des Preises mit der Tradesize $\Delta A_k $ wächst.

Impermanent Loss

Impermanent Loss (IL) bezeichnet die Wertminderung eines Liquiditäts-Pools aufgrund einer Preisänderung der im Pool enthaltenen Token: Beim Preisangleich an eine bei anderem Pool erfolgende Preisänderung nimmt ein Pool denjenigen Token auf, der im Preis gefallen ist und gibt denjenigen ab, der im Preis gestiegen ist. Da dies zu den urpsrünglichen Preisen des Pools passiert und nicht zu den sich extern ändernden Preisen, gibt der Pool einen größeren Wert her, als ihm zugeführt wird. Sobald die Preisänderung aber wieder rückgängig gemacht wird, wird auch die Wertminderung wieder ausgeglichen, daher "Impermanent".

IL und Slippage können in einer Vielzahl von Systemen miteinander in Zusammenhang gebracht werden: je größer die Slippage, desto geringere Token-Flüsse sind nötig, um einen Preisangleich zu bewirken und desto geringer ist in der Regel der IL.

Graphentheoretische Darstellungen

Ein Teil der Komplexität der Zusammenhänge kann durch eine gut gestaltete grafische Darstellung verborgen werden.

The asset conversion graph

Auf viele Token System hat Arbitrage großen Einfluss und muss gut untersucht werden. Der Asset-Umwandlungsgraph erlaubt eine einfache Erkennung von Arbitrage-Zyklen.

Jeder Graph $G=(V,E)$ besteht aus einer Menge an Knoten $V$ und einer Menge an Kanten $E$. Für den Assetumwandlungsgraph wird für jeden relevanten Token ein Knoten eingefügt. Für jede definierte Preisfunktion $\;_\alpha p_i^k$ wird eine Kante $\alpha$ vom Knoten $k$ zum Knoten $i$ eingefügt. Damit entspricht jede Kante einer Möglichen Zustandsänderung, bzw. einem Swap. Unterschiedliche Kanten können die gleiche Bezeichnung tragen. Zur genaueren Unterscheidung kann die Bezeichnung um den jeweiligen Operator erweitert werden: $\alpha.operator(...)$.

Betrachten wir beispielsweise ein auf Polygon eingesetztes System in dem drei verschiedene Token Verwendung finden: MATIC, DAI und der Token eines zu entwickelnden "TKN" eines zu entwickelnden Systems. Die Knoten des Graphen sind damit gegeben durch $V=\{MATIC, DAI, TKN\}$. Wir nehmen die Existenz eines UniSwap Pools für MATIC und DAI an. TKN kann direkt bei betrachtetem System für DAI erworben und für MATIC wieder verkauft werden. Der entsprechende Assetumwandlungsgraph ist gegen durch

$V=\{MATIC, DAI, TKN\} $

$E=\{MATIC\leftrightarrow DAI, DAI\rightarrow TKN, TKN \rightarrow MATIC\} $

und im Folgenden abgebildet.

Ein Kantengewicht, durch Kantendicke veranschaulicht, kann eingeführt werden, um Slippage darzustellen: je geringer die Slippage, desto dicker die Kante. Je dicker die Kante, desto dominanter ist die betrachtete Operation bei der Preisgebung.

Oft ist es von Relevanz, wer als Preisgeber und wer als Preisnehmer fungiert. Die Kantendicke erlaubt eine diesbezügliche Untersuchung: Entlang eines gegebenen Pfades fungiert der Operator mit dickster Kante als dominanter Preisgeber, Operatoren dünnerer Kanten als Preisnehmer.

Mögliche Arbitrage Zyklen sind durch geschlossene Pfade gegeben. Für den gegebenen Graphen können wir Arbitrage erwarten wenn

$\;_\text{Uni} p^\text{DAI}_\text{MATIC} < \;_\text{System} p^\text{DAI}_\text{TKN} * \;_\text{System} p^\text{TKN}_\text{MATIC}. $

Sie gehen mit folgenden Token Flüssen einher:

$\Delta\;^\alpha_\text{System} A_\text{DAI}>0 $

$\\ $

$\Delta\;^\text{System}_\alpha A_\text{MATIC}>0$,

wobei ein Agent mit Adresse $\alpha$ als Arbitrageur fungierte. Von den unterschiedlichen Kantendicken können wir ableiten, dass der Fluss durch UniSwap größer wäre, als der Fluss durch unser betrachtetes System.

Im angeführten Beispiel würde das System als eine Volatilitäts-getrieben Pumpe fungieren, die DAI ins System und MATIC aus dem System pumpt bis kein MATIC mehr im System verfügbar ist.

Der Tokenflussgraph

Gesamt- und Umlaufmenge sind wichtige Größen für Token Systeme: Ihre Entwicklung hängt maßgeblich davon ab, wie inflationär oder deflationär die jeweiligen Token sind. Erzeugungs- und Vernichtungsereignisse korrespondieren zu Sendern und Empfängern von Token.

Der Flussgraph beginnt mit dem Einfügen eines 0-Knoten, der als Quelle und Senke von Token fungiert. Für die verschiedenen Token werden eigene Kantenmengen eingeführt, die durch Farbgebund voneinader unterschieden werden können. Jede Kante entspricht einem Operator, der von einem bestimmten Agenten aufgerufen wird. Damit beschreibt jede Kante die Interaktion eines Agenten mit einem Contract. Die Knoten des Graphen werden anhand möglicher Rollen der Agenten bestimmt: jeder Rolle entspricht ein Knoten.

Für zuvor beschriebenes System ist die Rolles des "Traders" definierbar. Der Flussgraph zuvor beschriebenen Systems ist folgend dargestellt.

Der Graph zeigt, wie sich Token durch die verschiedenen Subsysteme oder von Agent zu Agent bewegen. Für stabile Systeme sollte jeder Pfad der beim 0-Knoten beginnt zu diesem zurückkehren. Dies ist für abgebildeten Graphen erfüllt. Ein weiteres Stabilitätskriterium verlangt, dass zu jedem in einen Knoten einlaufende Kante eine auslaufende Kante gleicher Farbe existieren sollte. Dies ist bei vorliegendem Graphen nicht der Fall: DAI fließt in das System ohne wieder abfließen zu können und MATIC fließt ab, ohne zufließen zu können.